- Instructor's Guide for D. Poole's Linear Algebra,
Brookes/Cole, (2005), ISBN 0-534-99861-5.
- Instructor's Guide for D. Poole's Linear Algebra
Second edition, Brooks/Cole | Cengage Learning, (2011) online access only.
- The geometry of minimal shape-preserving projections,
with B.L. Chalmers, Computers Math. Applic. 30(1995), No. 3-6, 277-281.
- Codimension one minimal projections onto the quadratics:
J. Approx. Theory, 85(1996), 27-42.
- A farthest-point characterization of the relative
Chebyshev center, with R. Huotari, Bull. Austral. Math. Soc., 54(1996), 27-33.
- Minimal shape-preserving projections onto
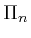
 , with B.L. Chalmers, Numer. Funct. Anal. and Optimiz.,
18(1997), 507-520.
, with B.L. Chalmers, Numer. Funct. Anal. and Optimiz.,
18(1997), 507-520.
- The Bernstein operator is the closest positive operator
to a projection, with B.L. Chalmers, D. Leviatan,
Approximation Theory IX, Volume 1: (Nashville, TN, 1998), 75-82, Vanderbilt
University Press.
- Existence of shape preserving A-action operators,
with B.L. Chalmers, Rocky Mountain J. Math., 28(1998), No. 3, 813-833.
- Optimal interpolating spaces preserving shape, with
B.L. Chalmers, D. Leviatan, J. Approx. Theory, 98(1999), 354-373.
- On
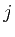 -convex preserving interpolation operators,
J. Approx. Theory 104(2000), 77-89.
-convex preserving interpolation operators,
J. Approx. Theory 104(2000), 77-89.
- Constrained optimal location, with R. Huotari, Numer. Funct. Anal. and
Optimiz. 22(1&2)(2001), 69-78.
- Optimal location with convex constraints, with R. Huotari
and J. Ribando, Approximation Theory X: Abstract and
Classical Analysis, (C.Chui,
L. Schumaker, J. Stoeckler eds.), Vanderbilt Press (2002), 239-246.
- On a constrained optimal location algorithm, with R. Huotari, J. of
Computational Analysis and Applications, 5, No. 1, (2003).
- Simplicial cones and the existence of shape-preserving
cyclic operators, Linear Algebra and its Applications, 375
(2003), 157-170.
- Codimension-one minimal projections onto Haar subspaces,
with G. Lewicki, J. Approx. Theory, 127 (2004), 198-206.
- A characterization and equations for
minimal shape-preserving projections, with B. Chalmers and
D. Mupasiri, J. Approx. Theory, 138 (2006), 184 - 196.
- A note on the existence of shape-preserving
projections, with D. Mupasiri, Rocky Mountain J. Math.,
37(2007), No. 2, 573-585.
- Minimal shape-preserving projections onto
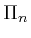 :
Generalizations and Extensions, with G. Lewicki,
Numer. Funct. Anal. and Optimiz., 27(2006), No. 7-8, 847-874.
:
Generalizations and Extensions, with G. Lewicki,
Numer. Funct. Anal. and Optimiz., 27(2006), No. 7-8, 847-874.
- A Lower Bound of the Strongly Unique Minimal Projection Constant of
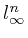 ,
, 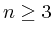 , with W. Odyniec, J. Approx. Theory, 145(2007), No. 1, 111-121.
, with W. Odyniec, J. Approx. Theory, 145(2007), No. 1, 111-121.
- Minimal multi-convex projections, with G. Lewicki, Studia
Math. 178(2007), No. 2, 99-124.
- On Three Forgotten Results of S. Krein, N. Bogolyubov and V. Guarari
with Applications to Bernstein Operators, with W. Odyniec,
Vestn. Syktyvkar Unin., 1(2007), 16-24.
- On the difficulty of preserving monotonicity via
projections and related results, with D. Mupasiri,
Jaen J. Approx., 2 No. 1 (2010), 1-12.
- Shape-preserving projections in tensor product spaces,
with G. Lewicki, J. Approx. Theory, 162 No. 5 (2010), 931-951.
- Shape-preserving projections in
low-dimensional settings and the
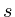 -monotone case, with I. Shevchuk,
Ukrainian Math. J., 5(2012), 674-684.
-monotone case, with I. Shevchuk,
Ukrainian Math. J., 5(2012), 674-684.
- Yet another generalization of a celebrated inequality of the
Gamma function, with E.M. Garcia-Caballero and S.G. Moreno,
Amer. Math. Monthly 120 (2013), 821.
- New Viete-Like Infinite Products of Nested Radicals with
Fibonacci and Lucas Numbers, with E.M. Garcia-Caballero and
S.G. Moreno, The Fibonacci Quarterly, 52(2014), no. 1, 27-31.
- The Golden Ratio and Viete's Formula, with
E.M. Garcia-Caballero and S.G. Moreno, Teach. Math. Comp. Sci.,
12(2014), no. 1, 43-54.
- A complete view of Viete-like infinite products wwith
Fibonacci and Lucas Numbers,
E.M. Garcia-Caballero and S.G. Moreno, Applied Mathematics and Computation,
247(2014), 703-711.
- New Gauss-Laguerre quadrature rules, with
E.M. Garcia-Caballero and S.G. Moreno, work in progress.
- Minimal
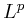 projections onto the lines, with G. Lewicki,
work in progress.
projections onto the lines, with G. Lewicki,
work in progress.
Michael Prophet
2015-04-30